3、移位运算
约 2860 字大约 10 分钟
2025-06-18
逻辑移位运算的对象是无符号数 左移:高位移除,低位补0 右移:低位移除,高位补0
先创建一个8位无符号变量,最低位b0的初始值为1,其他位的初始值为0,然后把该变量逻辑左移六位,再按位取反,得到101111,再与寄存器中的内容按位与运算就可以只清零b6位而不影响其他位 若想要改为b6位置1操作,可以左移6位(010000)后对寄存器的内容按位或操作
算术移位运算
算术移位运算的对象是有符号数(针对定点数,包括定点整数和定点小数) 不论正数还是负数,符号位保持不变,仅对数值位进行移位(左移或右移) 对真值的原码、反码和补码进行算术移位后,它们各自所对应的新的真值应该保持一致。 当真值为正数时,真值的原码、反码和补码都相同,因此,对它们进行算术移位后,它们各自所对应的新的真值自然是保持一致的。对于移位后出现的空位,规定添补0。 当真值为负数时,真值的原码、反码和补码都不同,因此,对它们进行算术移位后为了确保它们各自所对应的新的真值保持一致,对于移位后出现的空位,添补规则各不相同,
在未出现因丢位产生结果出错或精度缺失的情况下: n为位移次数 左移:乘以2n 右移:除以2n
对于有符号定点数的补码另一种以为方法 符号位也参与移位 左移:高位移除,低位补0,移动前后若符号位发生变化,则发生溢出 右移:低位移除,高位添补符号
优点: 左移时,有检测出发生溢出的方法:符号位发生变化可判定溢出 符号位与数值位一起移位,方便ALU处理
C语言中的移位运算 左移运算对应汇编指令中的逻辑左移,即高位移除,低位补0 右移运算根据操作数是无符号数还是有符号数分别对应汇编指令中的逻辑右移和算数右移 逻辑右移:将低位移除,高位补0 算数右移:低位移除,高位补原数据的符号位
循环移位
循环移位的对象是无符号数
将无符号数二进制形式中的各个位向左或向右移动,被移出的位会重新出现在另一端,形成循环在很多处理器架构中,循环移位指令会影响状态寄存器中的进位标志CF(Carry Flag)位,CF标志位用于标识在执行算术或逻辑操作时是否发生了进位。
根据CF标志位是否加入循环移位过程,循环移位可分为以下四种: 不带CF标志位的循环移位称为小循环
- 不带CF标志位的循环右移
- 不带CF标志位的循环左移 带CF标志位的循环移位称为大循环
- 带CF标志位的循环右移
- 带CF标志位的循环左移 不管带不带CF标志位CF标志位都是存在的,在不带CF标志位的循环移位中,CF标志位存储被移出的数
带CF标志位的循环移位中,CF标志位本身也存储有一个数据也参与移位运算,就相当于多了一个位
循环移位的应用 加密算法、哈希函数、优化算法
- 加密算法: 通过循环移位可以实现数据的混淆和置换,增强加密算法的安全性
- 哈希函数: 通过循环移位可以用来改变输入数据的排列顺序,以产生不同的哈希值,有利于增强哈希函数的混淆性和扩散性。
- 优化算法: 在某些算法中,循环移位可以用于优化性能和节省资源。例如,在图形处理和数字信号处理中,循环移位可以用于加速算法的执行。
循环移位的C语言实现 C语言中并没有直接提供循环移位操作符 通常情况下,可以使用移位运算操作符(例如:左移“<<”或右移“>>”)和位运算操作符(例如:或运算“|”)来实现。
#include <stdio.h>
//循环左移
unsigned int circularLeftShift(unsigned int value, int n){
return(value<<n)|(value>>(32-n));
}
//循环右移
unsigned int circularRightShift(unsigned int value, int n){
return(value >>n)|(value<<(32-n));
}
int main(){
unsigned int usi= 0x12345678;//待循环移位的32位无符号整数
int d = 4;//移位距离(即一次循环移动几位)
printf("0riginal value: 0x%x\n", usi);
printf("Circular left shift by %d bits:0x%x\n",d,circularLeftShift(usi, d));
printf("Circular right shift by %d bits:0x%x\n",d,circularRightShift(usi, d));
return 0;
}定点数的加法和减法运算
补码加减法运算公式
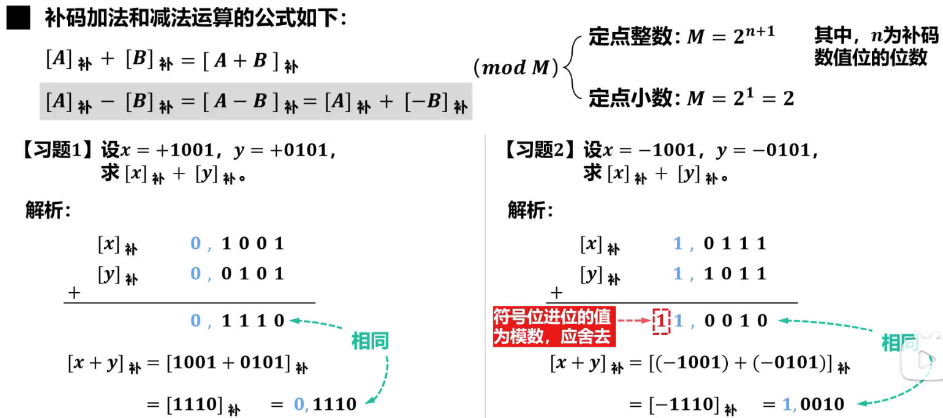
补码加减法溢出检测
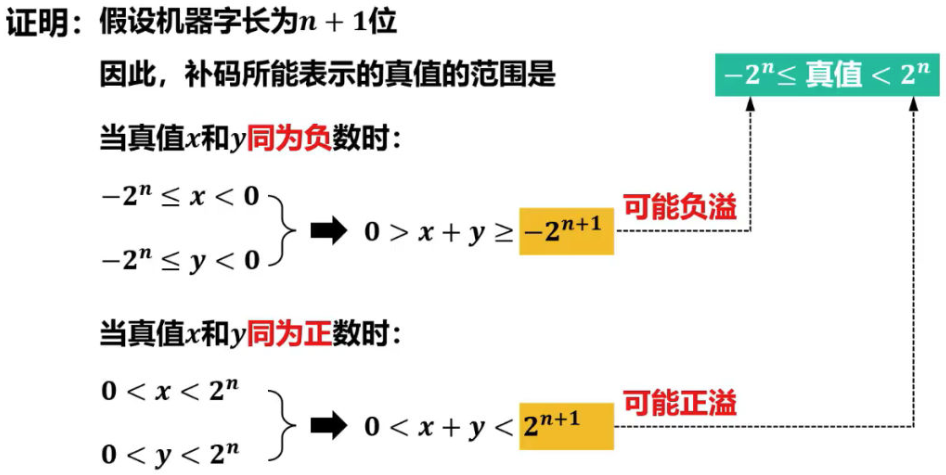
计算机的字长是有限的,因此所能表示的数据范围也是有限的。 当运算结果超出所能表示的数据范围时,就会出现溢出(Overflow)。 溢出会导致错误的运算结果。 计算机系统设计人员必须要解决溢出的检测问题,以便在发生溢出时计算机能做出相应的处理。
根据操作数的符号位与运算结果的符号位是否一致进行判断


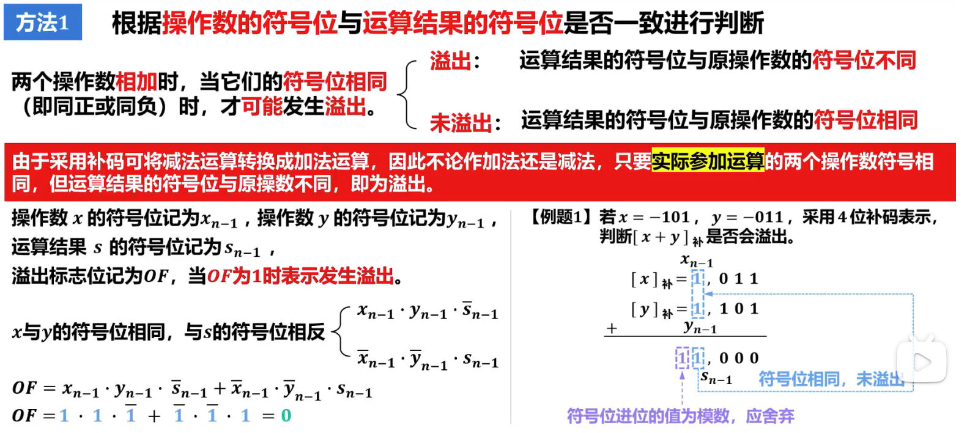
根据运算过程中最高数值位的进位和符号位的进位是否一致进行判断
不同可判定为产生溢出,相同可判定为没有产生溢出

最高数值位的进位记为Cn−1符号位的进位记为Cn 溢出标志位记为OF,当OF为1时表示发生溢出;Cn-1与 Cn不同,则产生溢出(即OF为1):OF=Cn−1⊕Cn
利用变形补码(具有2位符号位的补码)的符号位进行判断
变形补码也称为双符号补码,具有2个符号位,其余与补码相同
- 双符号位为00时,表示正数
- 双符号位为11时,表示负数
- 双符号位为01时,表示正溢出
- 双符号位为10时,表示负溢出 溢出判断非常直观,适合手工运算时的溢出检测,但其硬件成本高,需要额外准备机器字长存储双符号位,在计算机中主要采用单符号溢出检测方案。
[!warning] Title 负数变形补码转换成原码仍可以使用反码法或扫描法。

定点数的加减法运算
全加器的硬件逻辑实现
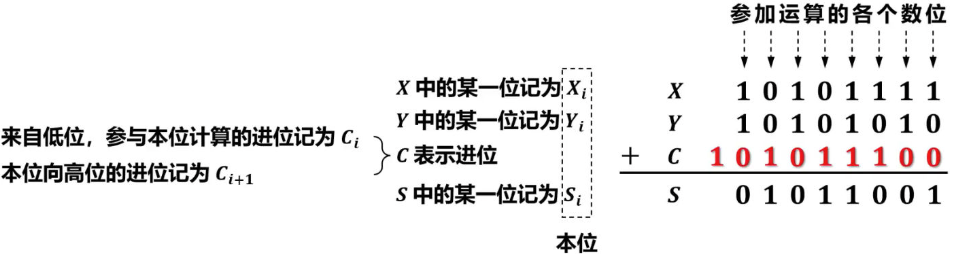
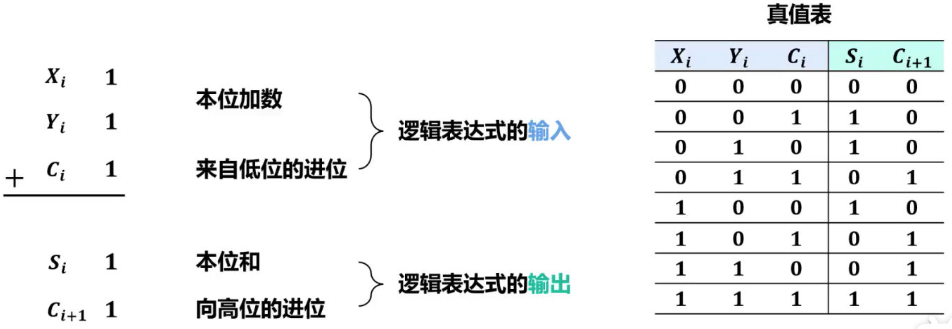
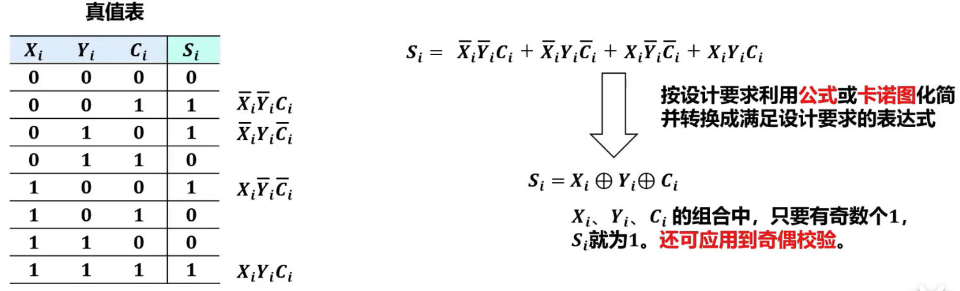
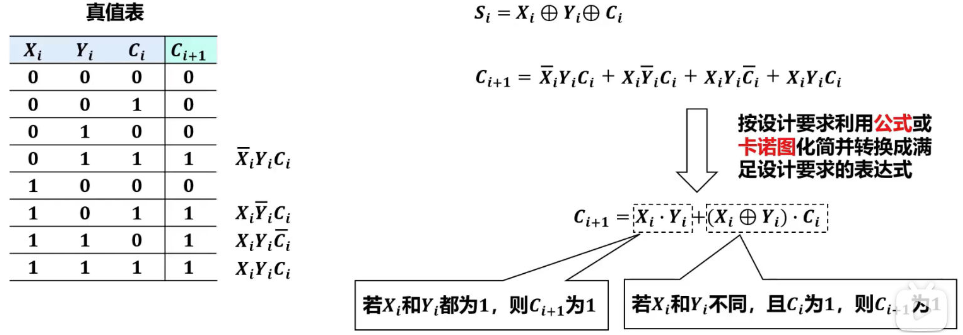
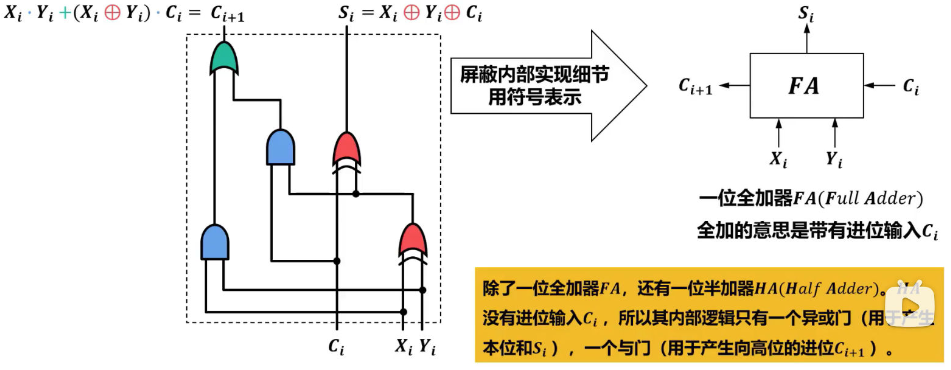
串行进位加法器
也叫行波进位加法器 可以使用n个全加器FA通过进位串联得到n位串行进位加法器 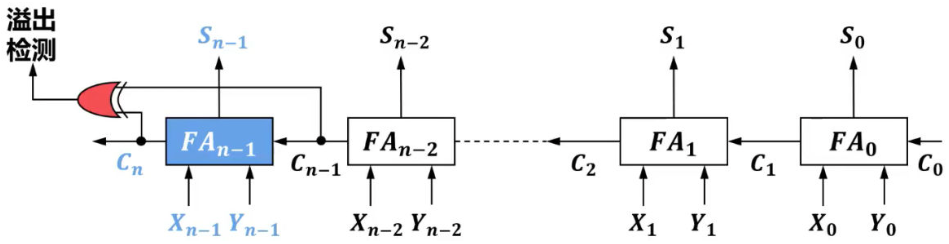 为了让n位串行进位加法器具有溢出检测功能,需要添加一个异或门将最高数值位的进位信号连接到异或门的一个输入端,将符号位的输出信号连接到异或门的另一个输入端,这样就可以使用最高数值位的进位与符号位的进位是否一致进行判断,异或门的输出就是检测结果
为了让n位串行进位加法器具有溢出检测功能,需要添加一个异或门将最高数值位的进位信号连接到异或门的一个输入端,将符号位的输出信号连接到异或门的另一个输入端,这样就可以使用最高数值位的进位与符号位的进位是否一致进行判断,异或门的输出就是检测结果
如果要是串行进位加法器能够实现补码的减法 根据[x]补−[y]补=[x]补+[−y]补 可以将异或门的输出端连接到y端上,异或门的一个输入即为原来的y端,另一个输入端和其他位上的异或门连到一条线上(称为sub端),当sub输入为1时各位上输出到全加器上的结果就是对y端的取反,当sub端输入为0时各位上输出到全加器上的结果就是y端原本的数据。再将sub端连接到FA0,也就是末位的加法器的C0端时当sub输入为1时就可以实现对y端输入的按位取反再加1,由此将y转为-y的补码进行加法运算。当sub端输入为0时没有取反也没有加1因此也不影响加法器的加法运算 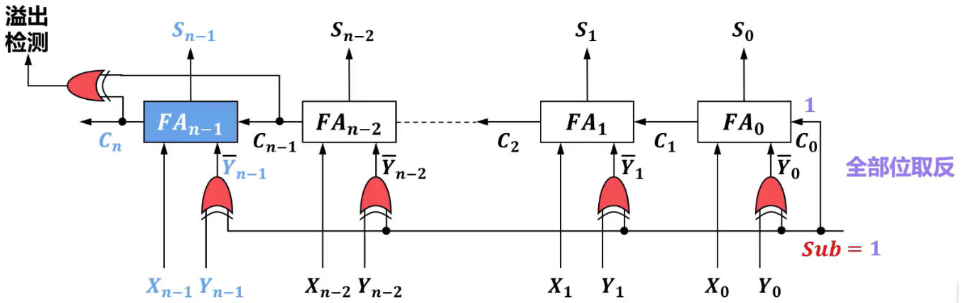 性能 由于每个高位的一位全加器的运算依赖于其相邻低位的一位全加器的进位输出,因此,所有一位全加器不能并行运算,其时间关键延迟,也就是输出所有本位和所需的时间(2n+4)T,这与串行进位加法器的位数n成线性关系。
性能 由于每个高位的一位全加器的运算依赖于其相邻低位的一位全加器的进位输出,因此,所有一位全加器不能并行运算,其时间关键延迟,也就是输出所有本位和所需的时间(2n+4)T,这与串行进位加法器的位数n成线性关系。
先行进位加法器
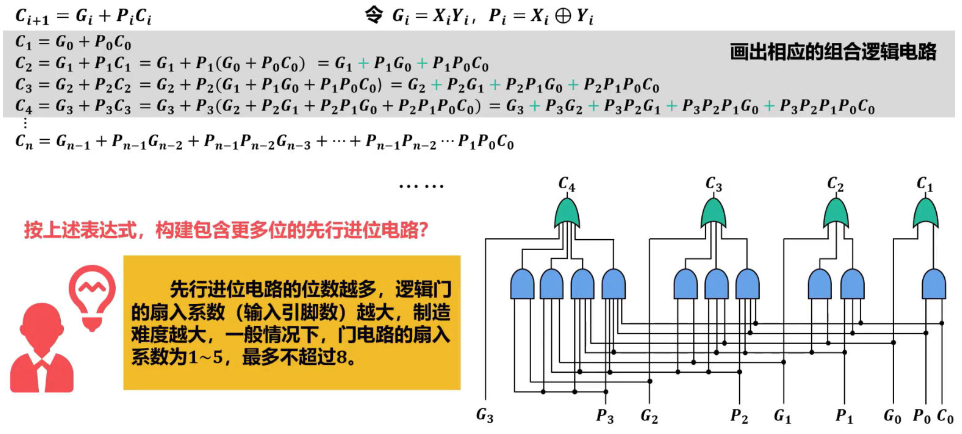
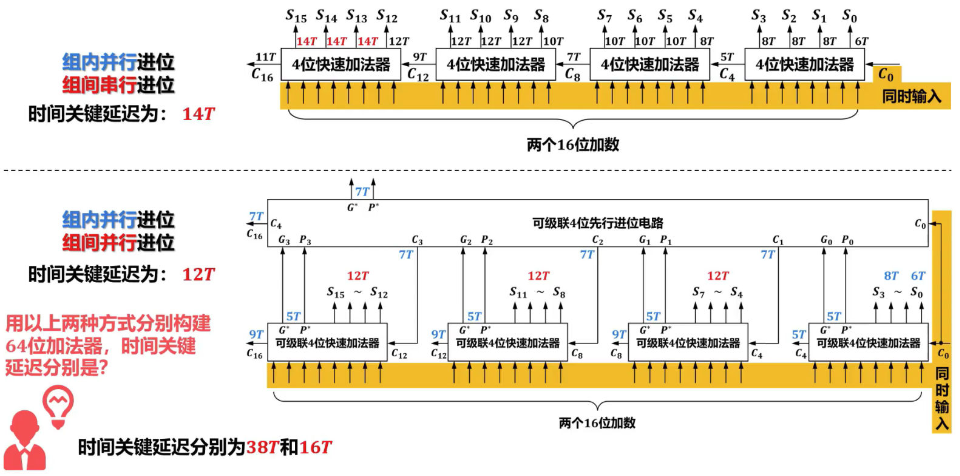
因此先行进位电路通常采用四位一组 四位快速加法器 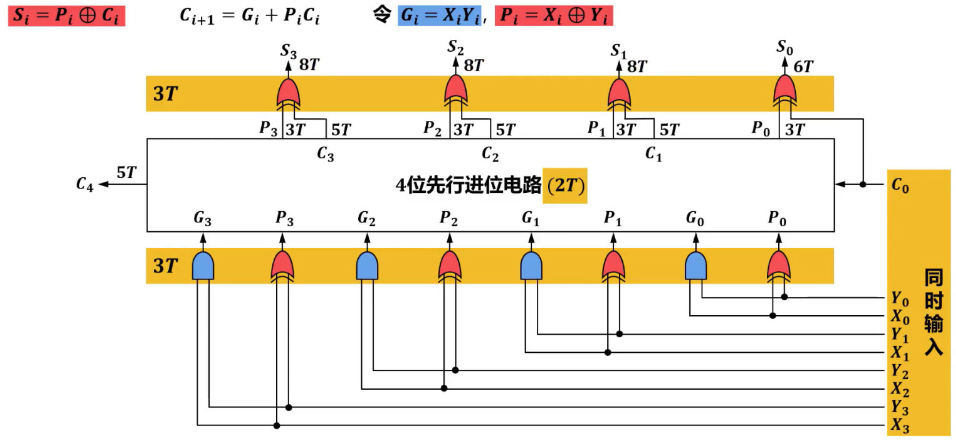 四位一组,组内并行进位、组间串行进位的16位加法器
四位一组,组内并行进位、组间串行进位的16位加法器
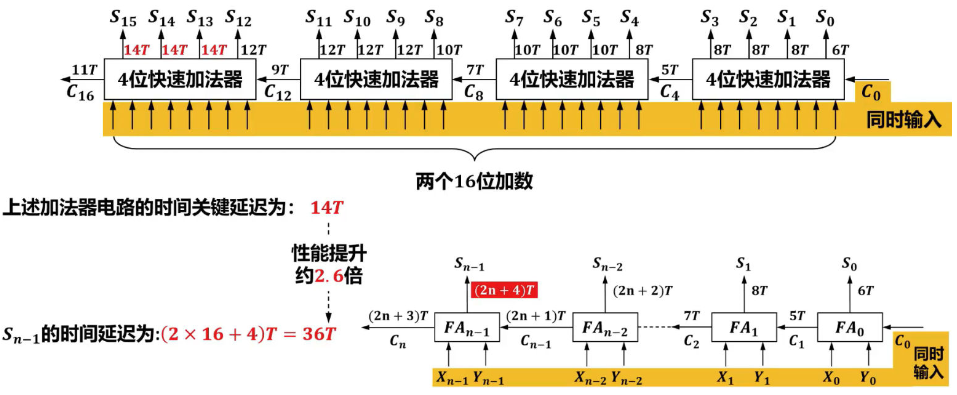
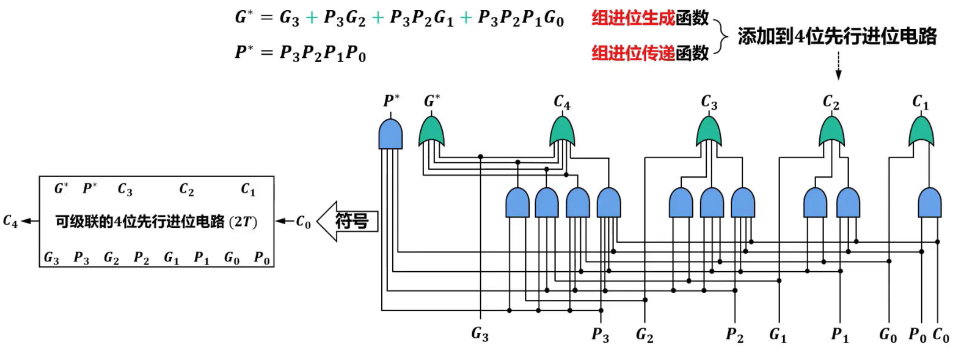
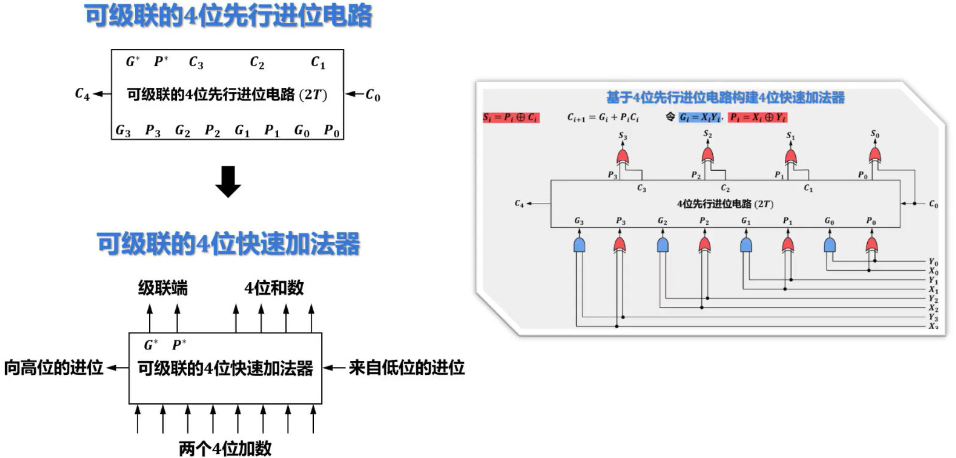
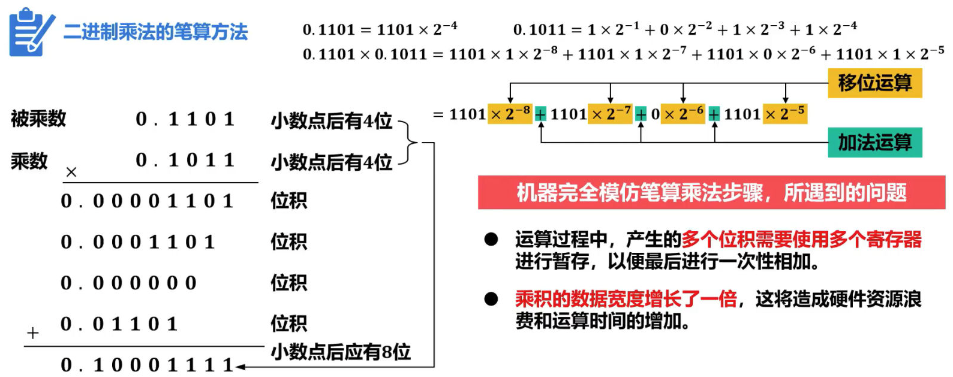
无符号数乘法
乘法运算可以由移位运算和加法运算配合完成
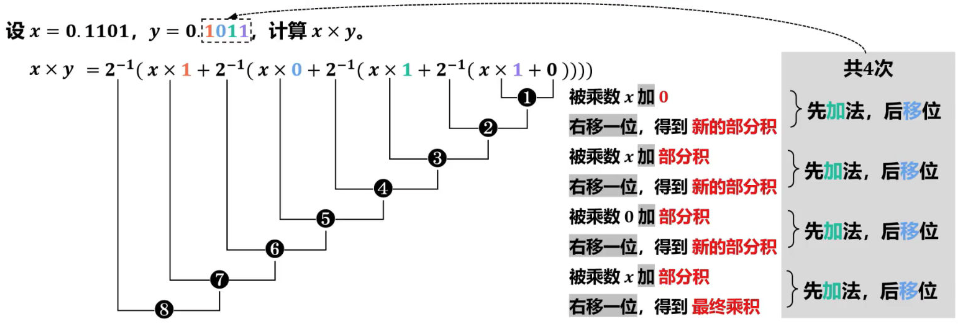
 针对以上问题对笔算乘法进行改进
针对以上问题对笔算乘法进行改进

 需要一个位宽为4位的寄存器存放被乘数x;还需要两个位宽为4位的寄存器分别存放部分积和最终乘积的高位和低位,初始阶段高位寄存器被清!,低位寄存器存放乘数y。再配上加法器及其他相应电路,即可实现乘法运算。
需要一个位宽为4位的寄存器存放被乘数x;还需要两个位宽为4位的寄存器分别存放部分积和最终乘积的高位和低位,初始阶段高位寄存器被清!,低位寄存器存放乘数y。再配上加法器及其他相应电路,即可实现乘法运算。 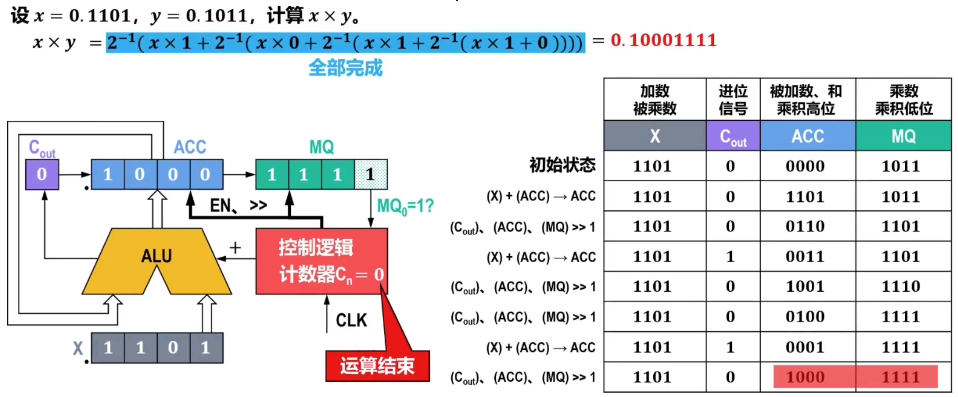
定点数的原码乘法运算
由于原码表示与无符号数非常类似,仅比无符号数多一个符号,而乘积的符号可以通过参与运算的两个数各自符号的逻辑异或求得,因此,上述无符号数乘法运算的硬件逻辑实现,可用于原码一位乘法仅需添加符号位处理即可。 一位乘法:并不是指参与乘法运算的两个操作数都是一位的,而是指在乘法运算过程中,每次根据乘数中的一位来计算位积
 这样符号位进行异或计算后得到运算结果的符号位,与原码分离而二者数据位部分可以直接当作无符号定点小数进行计算
这样符号位进行异或计算后得到运算结果的符号位,与原码分离而二者数据位部分可以直接当作无符号定点小数进行计算
定点数的补码定点运算
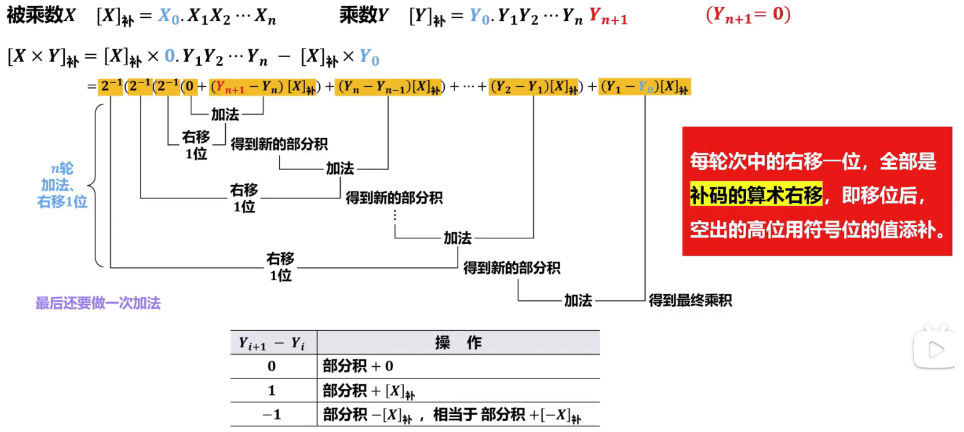
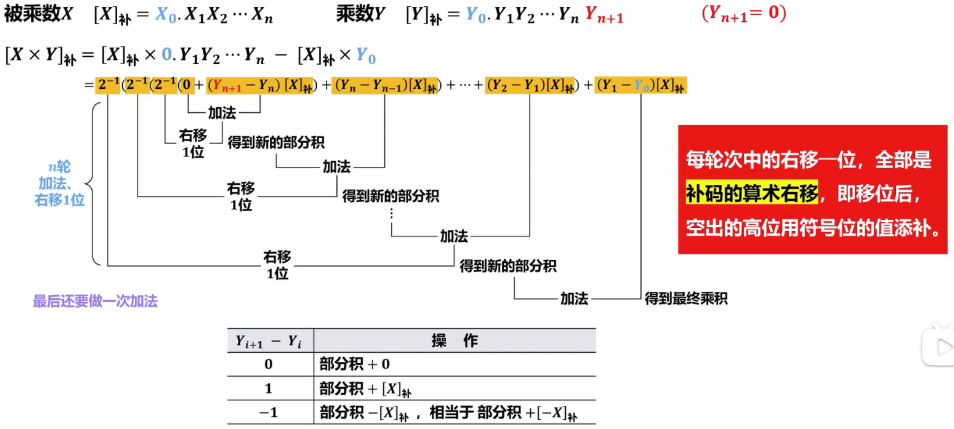
由于计算机中采用补码表示数据,如果用原码乘法计算两个数的乘积,则运算前需要将补码转换为原码、运算后还需要将原码再转换为补码,这样会增加许多操作步骤。为了减少处理环节,英国的布斯(Booth)夫妇于1950年提出了一种补码乘法,又称为Booth算法




贡献者
版权所有
版权归属:wynnsimon