2 树形结构
树和森林的转换
二叉树
二叉树的遍历
先序遍历,中序遍历,后序遍历的方法差不多只需要把printf和递归左右节点交换位置即可
// 先序遍历
void preOrder(TreeNode *root) {
if (root == NULL)
return;
printf("%c ", root->data);
preOrder(root->left);
preOrder(root->right);
free(root);
}非递归的实现需要借助栈(递归实现本质也是依靠栈)
层序遍历则需要借助一个队列来实现
// 二叉树节点
typedef struct TreeNode {
char data;
struct TreeNode *left;
struct TreeNode *right;
int lflag;
int rflag;
} TreeNode;
TreeNode *create_Node(char data) {
TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
node->data = data;
node->left = node->right = NULL;
node->lflag = 0;
node->rflag = 0;
return node;
}
// 队列节点
typedef struct QueueNode {
TreeNode *element;
struct QueueNode *next;
} QueueNode;
// 队列
typedef struct Queue {
QueueNode *front;
QueueNode *rear;
} Queue;
bool initQueue(Queue *queue) {
queue->front = queue->rear = NULL;
return true;
}
bool enqueue(Queue *queue, TreeNode *tnode) {
if (tnode == NULL)
return false;
QueueNode *node = (QueueNode *)malloc(sizeof(QueueNode));
node->element = tnode;
node->next = NULL;
if (queue->front == NULL)
queue->front = queue->rear = node;
else {
queue->rear->next = node;
queue->rear = node;
}
return true;
}
bool isEmpty(Queue *queue) {
return queue->front == NULL;
}
QueueNode *dequeue(Queue *queue) {
// 检查队列是否为空，为空则返回NULL
if (queue->front == NULL)
return NULL;
QueueNode *node = queue->front;
queue->front = queue->front->next;
return node;
}
// 先序遍历
void preOrder(TreeNode *root) {
if (root == NULL)
return;
printf("%c ", root->data);
preOrder(root->left);
preOrder(root->right);
free(root);
}
void levelOrder(TreeNode *root) {
if (root == NULL)
return;
Queue queue;
initQueue(&queue);
enqueue(&queue, root);
QueueNode *node;
while (!isEmpty(&queue)) {
node = dequeue(&queue);
printf("%c ", node->element->data);
if (node->element->left != NULL)
enqueue(&queue, node->element->left);
if (node->element->right != NULL)
enqueue(&queue, node->element->right);
free(node);
}
printf("\n");
}线索化二叉树
线索化:即将叶子节点上空的左右节点分别指向自己的上一个元素和下一个元素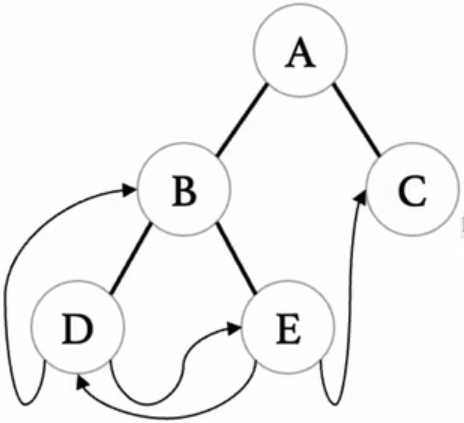 
在二叉树节点中设置两个标志位分别指示左右节点,如果标志位为0则表示该节点有元素,若为1表示该节点被线索化,其指向它的下一个元素 先序线索化
// 先序遍历 - 线索化二叉树
TreeNode *pre = NULL;
// 这里我们需要一个pre来保存后续结点的指向
void preOrderThreaded(TreeNode *root) { // 前序遍历线索化函数
if (root == NULL)
return;
if (root->left == NULL) { // 首先判断当前结点左边是否为NULL，如果是，那么指向上一个结点
root->left = pre;
root->lflag = 1; // 记得修改标记
}
if (pre && pre->right == NULL) { // 然后是判断上一个结点的右边是否为NULL，如果是那么进行线索化，指向当前结点
pre->right = root;
pre->rflag = 1; // 记得修改标记
}
pre = root; // 每遍历完一个，需要更新一下pre，表示上一个遍历的结点
if (root->lflag == 0) // 注意只有标志位是0才可以继续向下，否则就是线索了
preOrderThreaded(root->left);
if (root->rflag == 0)
preOrderThreaded(root->right);
}遍历先序线索化二叉树
/**
* @brief 遍历先序线索化二叉树
* @param root 根节点
* @note 只能适用于先序线索化的二叉树
*/
void preOrderThreaded(TreeNode *root) {
while (root != NULL) {
printf("%c ", root->data);
if (root->lflag == 0)
root = root->left;
else
root = root->right;
}
}中序线索化二叉树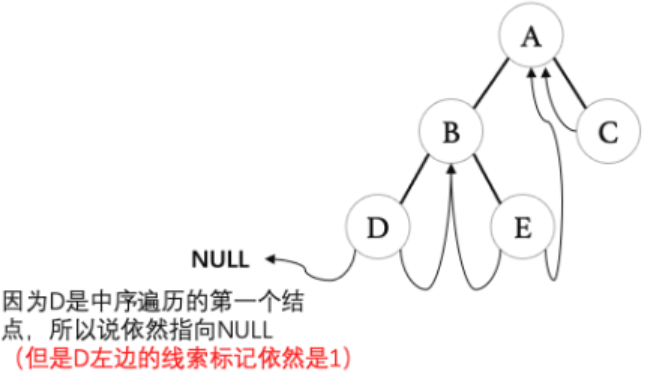 
// 中序遍历 - 线索化二叉树
TreeNode *pre = NULL;
void midOrderThreaded(TreeNode *root) {
if (root == NULL)
return;
if (root->lflag == 0)
midOrderThreaded(root->left);
if (root->left == NULL) {
root->lflag = 1;
root->left = pre;
}
if (pre && pre->right == NULL) {
pre->rflag = 1;
pre->right = root;
}
pre = root;
if (root->rflag == 0)
midOrderThreaded(root->right);
}遍历中序线索化的二叉树
/**
* 中序遍历 - 线索化二叉树
* @param root 根节点
* @note 只适用于中序线索化的二叉树
*/
void inmidOrderThreaded(TreeNode *root) {
while (root) {
while (root->lflag == 0) {
root = root->left;
}
printf("%c ", root->data);
while (root->rflag == 1) {
root = root->right;
printf("%c ", root->data);
}
root = root->right;
}
}后序线索化二叉树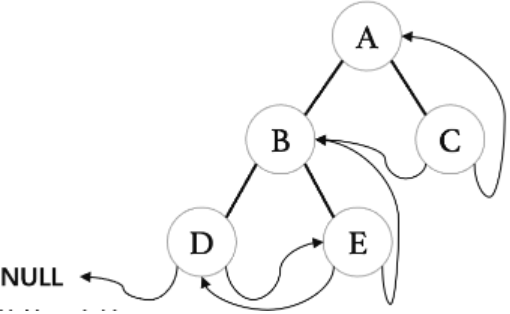 
// 后序遍历 - 线索化二叉树
TreeNode *pre = NULL;
void postOrderThreaded(TreeNode *root) {
if (root == NULL)
return;
if (root->left == NULL) {
root->left = pre;
root->lflag = 1;
}
if (root->lflag == 0)
postOrderThreaded(root->left);
if (root->rflag == 0)
postOrderThreaded(root->right);
if (pre && pre->right == NULL) {
pre->right = root;
pre->rflag = 1;
}
pre = root;
}遍历后序线索化的二叉树需要节点中有指向其父节点的指针
typedef struct TreeNode {
E element;
struct TreeNode * left;
struct TreeNode * right;
struct TreeNode * parent; //指向双亲（父）结点
int leftTag, rightTag;
} * Node;
void postOrder(Node root){
Node last = NULL, node = root; //这里需要两个暂存指针，一个记录上一次遍历的结点，还有一个从root开始
while (node) {
while (node->left != last && node->leftTag == 0) //依然是从整棵树最左边结点开始，和前面一样，只不过这里加入了防无限循环机制，看到下面就知道了
node = node->left;
while (node && node->rightTag == 1) { //左边完了还有右边，如果右边是线索，那么直接一路向前，也是跟前面一样的
printf("%c", node->element); //沿途打印
last = node;
node = node->right;
}
if (node == root && node->right == last) {
//上面的操作完成之后，那么当前结点左右就结束了，此时就要去寻找其兄弟结点了，我们可以
//直接通过parent拿到兄弟结点，但是如果当前结点是根结点，需要特殊处理，因为根结点没有父结点了
printf("%c", node->element);
return; //根节点一定是最后一个，所以说直接返回就完事
}
while (node && node->right == last) { //如果当前结点的右孩子就是上一个遍历的结点，那么一直向前就行
printf("%c", node->element); //直接打印当前结点
last = node;
node = node->parent;
}
//到这里只有一种情况了，是从左子树上来的，那么当前结点的右边要么是线索要么是右子树，所以直接向右就完事
if(node && node->rightTag == 0) { //如果不是线索，那就先走右边，如果是，等到下一轮再说
node = node->right;
}
}
}高级树结构
线索化二叉树
二叉查找树
要删除二叉搜索树上的节点需要尽量保证它的性质不丢失,高度不增加
- 删除叶子节点: 直接删除即可
- 被删除节点只有一个子树: 将节点对应的指针连到被删除节点的孩子再删除即可
- 左右都有孩子: 将要删除节点的前驱(左子树中最大的元素)或后继(右子树中最小的元素)放到被删除节点的位置
TreeNode *insert1(TreeNode *root, int data) {
if (root) {
if (data < root->data) {
root->left = insert1(root->left, data);
} else if (data > root->data) {
root->right = insert1(root->right, data);
} else {
printf("重复插入\n");
}
} else {
root = create_Node(data);
}
return root;
}
TreeNode *find(TreeNode *root, int data) {
while (root) {
if (data < root->data)
root = root->left;
else if (data > root->data)
root = root->right;
else
return root;
}
return NULL;
}
TreeNode* delete(Node root, E target){
if(root == NULL) return NULL; //都走到底了还是没有找到要删除的结点，说明没有，直接返回空
if(root->element > target) //这里的判断跟之前插入是一样的，继续往后找就完事，直到找到为止
root->left = delete(root->left, target);
else if(root->element < target)
root->right = delete(root->right, target);
else { //这种情况就是找到了
if(root->left && root->right) { //先处理最麻烦的左右孩子都有的情况
TreeNode* max = findMax(root->left); //寻找左子树中最大的元素
root->element = max->element; //找到后将值替换
root->left = delete(root->left, root->element); //替换好后，以同样的方式去删除那个替换上来的结点
} else { //其他两种情况可以一起处理，只需要删除这个结点就行，然后将root指定为其中一个孩子，最后返回就完事
TreeNode* tmp = root;
if(root->right) { //不是左边就是右边
root = root->right;
} else {
root = root->left;
}
free(tmp); //开删
}
}
return root; //返回最终的结点
}平衡二叉树
// 二叉树节点
typedef struct TreeNode {
int data;
struct TreeNode *left;
struct TreeNode *right;
int height;
} TreeNode;
TreeNode *create_Node(int data) {
TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
node->data = data;
node->left = node->right = NULL;
node->height = 1;
return node;
}
int max(int a, int b) {
return a > b ? a : b;
}
int getHeight(TreeNode *root) {
if (root == NULL)
return 0;
return root->height;
}
// 右旋
TreeNode *rightRotate(TreeNode *root) {
TreeNode *tmp = root->left;
root->left = tmp->right;
tmp->right = root;
root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
tmp->height = max(getHeight(tmp->left), getHeight(tmp->right)) + 1;
return tmp;
}
// 左旋
TreeNode *leftRotate(TreeNode *root) {
TreeNode *tmp = root->right;
root->right = tmp->left;
tmp->left = root;
root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
tmp->height = max(getHeight(tmp->left), getHeight(tmp->right)) + 1;
return tmp;
}
// 左右旋
TreeNode *leftRightRotate(TreeNode *root) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// 右左旋
TreeNode *rightLeftRotate(TreeNode *root) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
TreeNode *insert(TreeNode *root, int data) {
if (root == NULL) {
return create_Node(data);
} else if (data < root->data) {
root->left = insert(root->left, data);
root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
if ((getHeight(root->left) - getHeight(root->right)) > 1 || (getHeight(root->left) - getHeight(root->right)) < -1) {// 判断是否需要旋转
//因为是在左边节点插入的,失衡点必然在左边,所以只需要判断是否需要左旋或者左右旋
if (getHeight(root->left->left) > getHeight(root->left->right)) {//LL型失衡
root = rightRotate(root);
} else {//LR型失衡
root = leftRightRotate(root);
}
}
} else if (data > root->data) {
root->right = insert(root->right, data);
root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
if ((getHeight(root->right) - getHeight(root->left)) > 1 || (getHeight(root->right) - getHeight(root->left)) < -1) {
if (getHeight(root->right->right) > getHeight(root->right->left)) {//RR型失衡
root = leftRotate(root);
} else {//RL型失衡
root = rightLeftRotate(root);
}
}
}
return root;
}红黑树
这里的叶子节点是空节点,空节点也算在规则内
- 根节点和叶子节点都是黑色
- 所有的红色节点其左右孩子都必须是黑色的(从上到下不能存在连续的红色节点)
- 任一节点到它的叶子节点所有路径上黑色节点数都相同
- 插入的节点默认是红色的
其他树结构
B树
B+树
哈夫曼树
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int weight;
char value;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
void initTreeNode(TreeNode *node, int weight, char value) {
node->weight = weight;
node->value = value;
node->left = NULL;
node->right = NULL;
}
TreeNode *createTreeNode(int weight, char value) {
TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
initTreeNode(node, weight, value);
return node;
}
// 优先队列节点
typedef struct QueueNode {
TreeNode *element;
struct QueueNode *next;
} QueueNode;
void initQueueNode(QueueNode *node, TreeNode *nodeData) {
node->element = nodeData;
node->next = NULL;
}
QueueNode *createQueueNode(TreeNode *nodeData) {
QueueNode *node = (QueueNode *)malloc(sizeof(QueueNode));
initQueueNode(node, nodeData);
return node;
}
int getWeight(QueueNode *node) {
if (node == NULL) {
return 0;
}
return node->element->weight;
}
void enqueue(QueueNode **queue, TreeNode *node) {
if (node == NULL) {
return;
}
QueueNode *newNode = createQueueNode(node);
if (*queue == NULL) {
*queue = newNode;
} else {
QueueNode *pre = NULL;
newNode->next = *queue;
while (newNode->next && getWeight(newNode) > getWeight(newNode->next)) {
pre = newNode->next;
newNode->next = newNode->next->next;
}
if (pre == NULL) {
*queue = newNode;
} else {
pre->next = newNode;
}
}
}
QueueNode *dequeue(QueueNode **queue) {
if (queue == NULL || *queue == NULL) {
return NULL;
} else {
QueueNode *temp = *queue;
*queue = temp->next;
return temp;
}
}
// 构造哈夫曼树
TreeNode *createHuffmanTree(QueueNode **queue) {
if (queue == NULL || *queue == NULL) {
return NULL;
}
TreeNode *temp1 = NULL, *temp2 = NULL;
while (*queue != NULL && (*queue)->next != NULL) {
temp1 = dequeue(queue)->element;
temp2 = dequeue(queue)->element;
TreeNode *newNode = createTreeNode(temp1->weight + temp2->weight, '\0');
newNode->left = temp1;
newNode->right = temp2;
enqueue(queue, newNode);
}
temp1 = dequeue(queue)->element;
return temp1;
}
// 哈夫曼编码
void huffmanEncode(TreeNode *root, int code) {
if (root == NULL) {
return;
}
if (root->left != NULL) {
huffmanEncode(root->left, (code << 1) | 0);
}
if (root->right != NULL) {
huffmanEncode(root->right, (code << 1) | 1);
}
if (root->left == NULL && root->right == NULL) {
printf("%c: %d\n", root->value, code);
}
}
int main() {
QueueNode *n1 = NULL;
enqueue(&n1, createTreeNode(5, 'A'));
enqueue(&n1, createTreeNode(16, 'B'));
enqueue(&n1, createTreeNode(8, 'C'));
enqueue(&n1, createTreeNode(13, 'D'));
TreeNode *tree = createHuffmanTree(&n1);
huffmanEncode(tree, 0);
return 0;
}堆和有限队列
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int weight;
char value;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode;
void initTreeNode(TreeNode *node, int weight, char value) {
node->weight = weight;
node->value = value;
node->left = NULL;
node->right = NULL;
}
TreeNode *createTreeNode(int weight, char value) {
TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
initTreeNode(node, weight, value);
return node;
}
// 优先队列节点
typedef struct QueueNode {
TreeNode *element;
struct QueueNode *next;
} QueueNode;
void initQueueNode(QueueNode *node, TreeNode *nodeData) {
node->element = nodeData;
node->next = NULL;
}
QueueNode *createQueueNode(TreeNode *nodeData) {
QueueNode *node = (QueueNode *)malloc(sizeof(QueueNode));
initQueueNode(node, nodeData);
return node;
}
int getWeight(QueueNode *node) {
if (node == NULL) {
return 0;
}
return node->element->weight;
}
void enqueue(QueueNode **queue, TreeNode *node) {
if (node == NULL) {
return;
}
QueueNode *newNode = createQueueNode(node);
if (*queue == NULL) {
*queue = newNode;
} else {
QueueNode *pre = NULL;
newNode->next = *queue;
while (newNode->next && getWeight(newNode) > getWeight(newNode->next)) {
pre = newNode->next;
newNode->next = newNode->next->next;
}
if (pre == NULL) {
*queue = newNode;
} else {
pre->next = newNode;
}
}
}
QueueNode *dequeue(QueueNode **queue) {
if (queue == NULL || *queue == NULL) {
return NULL;
} else {
QueueNode *temp = *queue;
*queue = temp->next;
return temp;
}
}
int main() {
QueueNode *n1= NULL;
enqueue(&n1, createTreeNode(5, 'A'));
enqueue(&n1, createTreeNode(16, 'B'));
enqueue(&n1, createTreeNode(8, 'C'));
enqueue(&n1, createTreeNode(13, 'D'));
while (n1 != NULL) {
QueueNode *temp = dequeue(&n1);
printf("%c\n",temp->element->value);
free(temp);
}
return 0;
}使用堆也可以实现优先队列,且因为堆的元素是有序的故经常使用数组实现堆 因为堆是完全二叉树,这样使用数组实现的堆其节点在查找自己的父节点时可以使用自身索引/2即可 得到父节点的索引,但必须要以索引为1为根节点,这样吧才不会出bug 堆不保证数组中的元素是有序的,但能保证首位元素是最大(大根堆)或最小(小根堆)的
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct Heap {
int* arr;
int size;
int capacity;
} Heap;
void initHeap(Heap* heap) {
heap->capacity = 10;
heap->size = 1; // 索引为0处不存数据
heap->arr = (int*)malloc(heap->capacity * sizeof(int));
}
void insert(Heap* heap, int val) {
if (heap == NULL || heap->size >= heap->capacity)
return;
heap->arr[heap->size++] = val;
for (int i = heap->size - 1; i > 1; --i) {
if (heap->arr[i] > heap->arr[i / 2]) {
int tmp = heap->arr[i];
heap->arr[i] = heap->arr[i / 2];
heap->arr[i / 2] = tmp;
}
}
}
int pop(Heap* heap) {
if (heap == NULL || heap->size <= 1)
return -1;
int ret = heap->arr[1];
heap->arr[1] = heap->arr[--heap->size];
for (int i = 1; i < heap->size && i * 2 + 1 < heap->size; ++i) { // 从根节点开始调整,和插入相反的顺序
if (heap->arr[i] < heap->arr[i * 2] || heap->arr[i] < heap->arr[i * 2 + 1]) {
int index = heap->arr[i * 2] > heap->arr[i * 2 + 1] ? i * 2 : i * 2 + 1;
int tmp = heap->arr[i];
heap->arr[i] = heap->arr[index];
heap->arr[index] = tmp;
}
}
return ret;
}
int main() {
Heap heap;
initHeap(&heap);
// 插入5,2,3,7,6
insert(&heap, 5);
insert(&heap, 2);
insert(&heap, 3);
insert(&heap, 7);
insert(&heap, 6);
insert(&heap, 8);
insert(&heap, 9);
for (int i = 1; i < heap.size; ++i) {
printf("%d ", heap.arr[i]);
}
printf("\n");
while (heap.size > 1)//每次出堆size都会减少所以不能使用for循环
printf("%d ", pop(&heap));
return 0;
}并查集
class UnionFind {
public:
vector<int> arr;
int size;
UnionFind(int n) : arr(n), size(n) {
for (int i = 0; i < n; ++i) {
arr[i] = -1;
}
}
int find(int x) {
if (x < 0)
return x;
if (arr[x] < 0)
return x;
int tmp = x;
while (arr[tmp] >= 0) {
tmp = arr[tmp];
}
arr[x] = tmp;
return tmp;
}
void unionSet(int x, int y) {
if (x < 0 || y < 0)
return;
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY)
return;
if (arr[rootX] > arr[rootY]) {
arr[rootY] += arr[rootX];
arr[rootX] = rootY;
} else {
arr[rootX] += arr[rootY];
arr[rootY] = rootX;
}
}
void foreach () {
for (int i = 0; i < size; ++i) {
cout << i << " " << arr.at(i) << endl;
}
}
};前缀树
class Trie {
public:
char val;
bool isEnd = false;
vector<Trie*> child = vector<Trie*>(26, nullptr);
void insert(string word) {
Trie* cur = this;
for (auto c : word) {
if (cur->child[c - 'a'] == nullptr) {
cur->child[c - 'a'] = new Trie();
cur->child[c - 'a']->val = c;
}
cur = cur->child[c - 'a'];
}
cur->isEnd = true;
}
bool search(string word) {
Trie* cur = this;
for (auto c : word) {
if (cur->child[c - 'a'] == nullptr)
return false;
cur = cur->child[c - 'a'];
}
return cur->isEnd;
}
bool startsWith(string prefix) {
Trie* cur = this;
for (auto c : prefix) {
if (cur->child[c - 'a'] == nullptr)
return false;
cur = cur->child[c - 'a'];
}
return true;
}
~Trie() {
for (auto child : this->child) {
if (child != nullptr)
delete child;
}
}
};
int main() {
Trie trie;
trie.insert("apple");
trie.insert("app");
trie.insert("banana");
cout << "Search 'apple': " << trie.search("apple") << endl; // 输出 1 (true)
cout << "Search 'app': " << trie.search("app") << endl; // 输出 1 (true)
cout << "Search 'banana': " << trie.search("banana") << endl; // 输出 1 (true)
cout << "Search 'appl': " << trie.search("appl") << endl; // 输出 0 (false)
cout << "StartsWith 'app': " << trie.startsWith("app") << endl; // 输出 1 (true)
cout << "StartsWith 'banan': " << trie.startsWith("banan") << endl; // 输出 1 (true)
cout << "StartsWith 'appl': " << trie.startsWith("appl") << endl; // 输出 0 (false)
return 0;
}贡献者
pinkdopeybug版权所有
版权归属：
